Publications

Collective Foraging and Behavioural Heterogeneity in Ants: First-Passage Statistics with Heterogeneous Walkers in a Honeycomb Lattice

Authors: D.M., Pol Fernández-López, Frederic Bartumeus, Luca Giuggioli

Journal: In Review (arXiv pre-print)

Summary:
We have present a theoretical model to quantify the foraging behaviour of the ant species Aphaenogaster senilis in laboratory experiments. The model extends known theory on correlated random walks to account for the underlying Y-maze (honeycomb) lattice and on the fFPT of N independent random walkers, allowing the population to be heterogeneous in behaviour. We show that scouts outperform recruits in both search and exploration, give indication of a central placed foraging behaviour and highlight that the characteristic fFPT time of the foraging ants corresponds to the timescale related to the mode of the fFPT distribution rather than its mean.

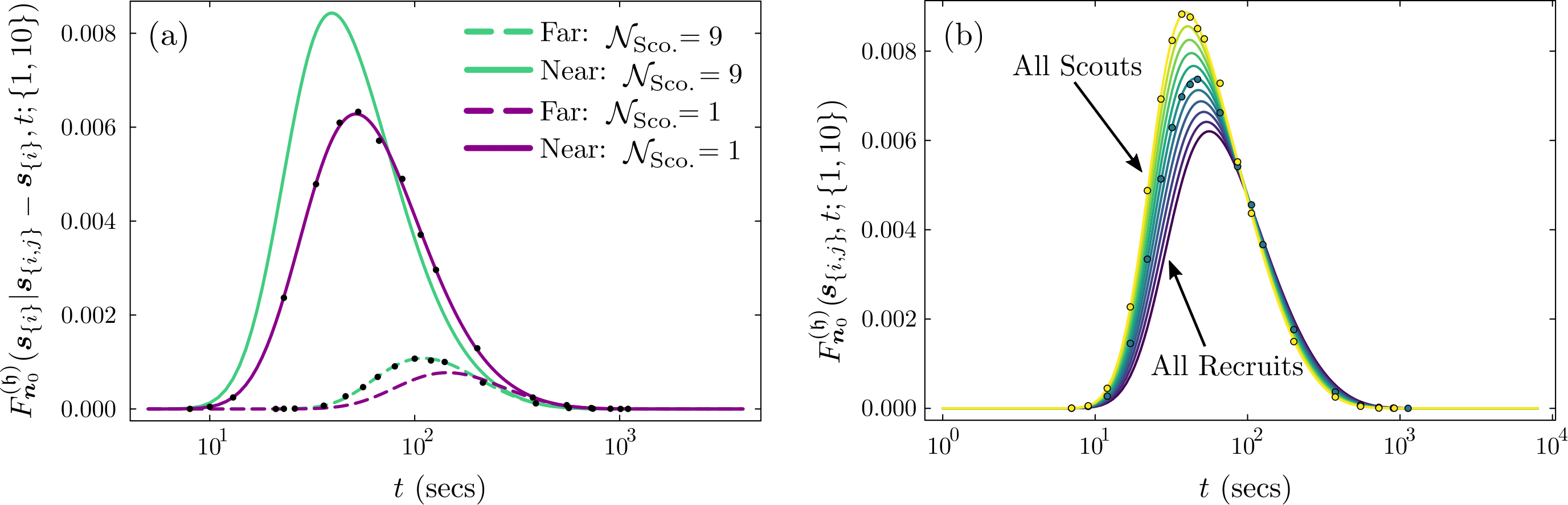
Nearby food source found first and scouts are more efficient searchers than recruits. — Here we show that the nearby food source will most likely be found first and that scouts are more efficient searchers than recruits.

Persistent and anti-Persistent Motion in Bounded and Unbounded Space: Resolution of the First-Passage Problem

Authors: D.M., Luca Giuggioli

Journal: New Journal of Physics, 26, (2024)

Summary:
Here we present an exact analytic framework to quantify search processes for the one-step memory extension of the random walk - the non-Markovian perisistent random walk. The theory is general and applicable in arbitrary dimension, with any boundary condition. This may find application in active matter, mathematical biology and movement ecology.

Bi-modal first-passage probability mass functions in bounded persistent random walks. — Here we uncovered the existence of bi-modal first-passage probality mass functions in bounded (reflecting and periodic) persistent random walks.

Multi-target search in bounded andheterogeneous environments: a lattice random walk perspective

Authors: Luca Giuggioli, Seeralan Sarvaharman, Debraj Das, D.M. and Toby Kay

Journal: To Appear in The Target Problem (Eds. D. S. Grebenkov, R. Metzler, G. Oshanin), Springer Nature (2024)

Summary:
Here we present a review of the latest advances in the field of search in heterogeneous and bounded lattice random walks. It was an absolute pleasure to work with such a lovely team.

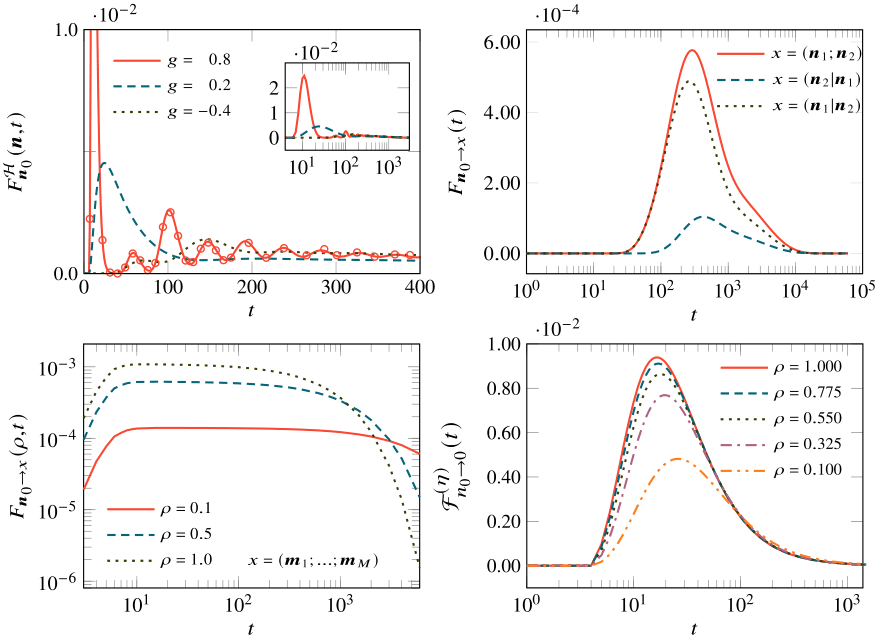
First-passage probability mass functions for hexagonal and square lattices with and without bias. — A collection of first-passage probability mass functions for hexagonal and square lattices with and without bias.

Exact spatiotemporal dynamics of lattice random walks in hexagonal and honeycomb domains

Authors: D.M., Seeralan Sarvaharman and Luca Giuggioli

Journal: Physical Review E, 107, 054139, (2023)

Summary:
Here we develop a general theory to describe, exactly, diffusive processes when the underlying geometry is hexagonal. We consider two lattices, the hexagonal lattice (coordination number six) and the non-Bravias honeycomb lattice (coordination number three). Modelling random movement on hexagonal structures is a modelling tool used in varying applications from exciton transport on the surface of carbon nanotubes to animal foraging theory.

Diffusive propagation over a six-sided hexagon with zig-zag periodic boundary condition for the honeycomb lattice. — The diffusive propagation over a six-sided hexagon with zig-zag periodic boundary condition for the honeycomb lattice.